zpět

Účinek síly na těleso otáčivé kolem pevné osy. Páka

 

V mnoha zařízeních se využívá otáčivých účinků síly (např. klika dveří, okno, nůžky, předloktí atd.)

Na čem tedy závisí otáčivý účinek síly?

 

Příklad1:

Představte si dvě situace, na houpačce se houpou dvě děti se stejnou hmotností a na druhé houpačce se houpe dítě s menší a větší hmotností.

POZORUJEME že, dětem se stejnou hmotností se houpe dobře, ovšem děti s rozdílnou hmotností mají problém (těžší dítě převažuje lehčí).

 

Příklad2:

Navazuje na předchozí příklad.

Jak mohou děti sedět na houpačce (dvě stejně těžké děti)? Jak si musí sednout děti na houpačce (těžší a lehčí dítě) aby se jim houpalo také dobře? Můžeme toto vysvětlit v pokusu s pravítkem (pravítkový model houpačky).

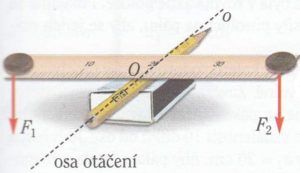
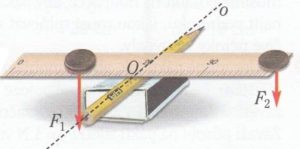
POZORUJEME že, aby se dětem s rozdílnou hmotností houpalo dobře, musí se těžší dítě posadit blíže ke středu houpačky.

 

Houpačka je příkladem zařízení kterému říkáme páka.

Páka – je tyč, která je otáčivá kolem osy.

V pokusu s pravítkem nám osu představuje přímka dotyku tužky s pravítkem.

Otáčivé účinky síly závisejí nejen na velikosti síly, ale také na tom, v jaké vzdálenosti od osy otáčení síla působí. Tuto vzdálenost nazýváme rameno síly.

 

Při pokusech a výpočtech je je výhodné zobrazit si páku zjednodušeně (schématicky).

a₁, a₂ jsou ramena síly, bod O je působiště síly (průsečík osy otáčení a páky), F₁, F₂ síly působící na houpačku (svisle dolů).

 

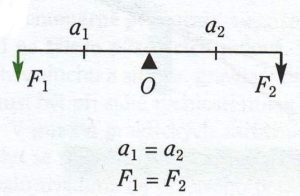
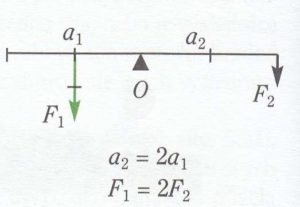
Aby byla páka v rovnovážné poloze, musí platit:

síla působící vlevo . rameno síly = síla působící vpravo . rameno síly

 

F₁ . a₁ = F₂ . a₂

 

Toto tvrzení je možné si ověřit na několika příkladech:

Páku upevníme tak aby se mohla otáčet okolo vodorovné osy procházející těžištěm.  Vlevo zavěsíme závaží např. o hmotnosti 100 g, páka se začne otáčet levým koncem dolů. Jaké závaží (o jaké hmotnosti) a jak daleko musíme dát toto závaží na druhou stanu páky aby zůstala v rovnovážné poloze?

 

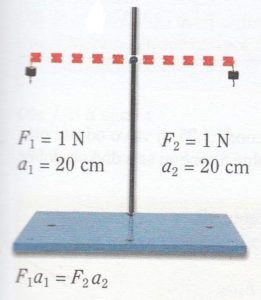
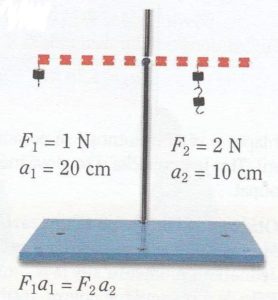
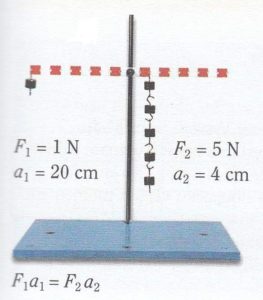
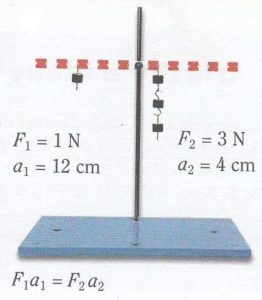
Z těchto pokusu vyplývá, že otáčivý účinek závisí na součinu velikosti síly a jejího ramene. Tento součin se nazývá moment síly (značíme písmenem M). Jednotka momentu síly je newtonmetr [N.m].

 

M = F . a

 

Podmínku rovnovážné polohy páky definujeme:

Páka je v rovnovážné poloze, jestliže se moment síly, která otáčí páku v jednom smyslu, rovná momentu síly, která otáčí páku v opačném smyslu.

 

zpět

---

Růžena KOLÁŘOVÁ, Jiří BOHUNĚK: Fyzika pro 7. ročník základní školy, dotisk 2. vydání, Havlíčkův Brod: nakladatelství Prometheus, spol. s.r.o., 2016. ISBN 978-80-7196-265-6