Měření délky s různou přesností

Pokus pro ověření:
Měříme kostičku lega měřidlem se stupnicí v cm, mm a pomocí posuvného měřidla s noniem.
POZORUJEME, že:
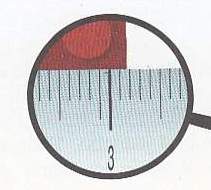
1) měřidlo se stupnicí v cm – na obrázku je vidět že d je v rozmezí 3 cm < d < 4 cm a je blíže k 3 cm, proto naměřenou hodnotu zaokrouhlíme na 3 a zapíšeme d = 3 cm. Odchylka měření je 0,5 cm.
Zaokrouhlený údaj se může lišit nejvýše o polovinu nejmenšího dílku = odchylka měření.
2) měřidlo se stupnicí v mm – na obrázku je vidět že d je v rozmezí 31 mm < d < 32 mm a je blíže k 32 mm, proto naměřenou hodnotu zaokrouhlíme na 32 a zapíšeme d = 32 mm. Odchylka měření je 0,5 mm.

3) měření posuvným měřidle s digitálním noniem – zjistíme hodnotu d = 31.84 mm.
Výsledek není nikdy přesný! Udává jen přibližnou hodnotu skutečné délky.
Opakované měření délky
Pro přesnost opakujeme měření alespoň 5x.
Skutečné délce se přibližuje nejvíce aritmetický průměr naměřených hodnot.
Opakování měření je vhodné zejména když je těžké určit jak měřidlo přiložit (př. víčko sklenice).
Pokus pro ověření:
Naměřili jsme délku kostky. Při opakovaném měření byly naměřeny tyto hodnoty: 6,45 – 6,47 – 6,45 – 6,48 – 6,46 m.
POZORUJEME, že skutečná délka je v rozmezí 6,45 m < d < 6,48 m. Přičemž 6,45 je dolní mez měření a 6,48 je horní mez měření.
Aritmetický průměr vypočteme:
d = (6,45 + 6,47 + 6,45 + 6,48 + 6,46) : 5 = 6,462 m
Podle zápisu byla všechna měření provedena s přesností na cm.
Proto aritmetický průměr zaokrouhlíme také s přesností na cm: d = 6,46 m.
CITACE: viz. odkaz: [k. 5 – fyzika], [obr. 285 – ve výstavbě]

